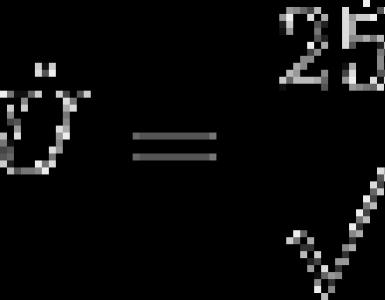Solving problems in electrical engineering (TOE). Solution of problems in electrical engineering (TOE) Solution of electrical engineering to order

To convert values ​​to actual ones you need to:

Dot above I means it is complex.

In order not to be confused with current, in electrical engineering a complex unit is denoted by the letter “j”.

For a given voltage we have:

When solving problems, they usually operate with effective values.

New elements are introduced in alternating current:

L – [Gn]
Capacitor [capacitance]	S – [F]

Their resistances (reactances) are found as:


(capacitor resistance is negative)

For example, we have a circuit, it is connected to a voltage of 200 V, having a frequency of 100 Hz. We need to find the current. Element parameters are set:

To find the current, you need to divide the voltage by the resistance (from Ohm's law). The main task here is to find resistance.

The complex resistance is found as:

We divide the voltage by the resistance and get the current.

All these actions are conveniently carried out in MathCad. The complex unit is put "1i" or "1j". If this is not possible, then:

1. It is convenient to do the division in exponential form.
2. Addition and subtraction - in algebraic.
3. Multiplication - in any way (both numbers in the same form).

Also, let's say a few words about power. Power is the product of current and voltage for DC circuits. For alternating current circuits, another parameter is introduced - the phase shift angle (or rather its cosine) between voltage and current.

Suppose we have found the current and voltage (in complex form) for the previous circuit.

Power can also be found using another formula:

In this formula is the conjugate current complex. Conjugate means that its imaginary part (the one with j) changes its sign to the opposite (minus/plus).
Re– means the real part (the one without j).

These were the formulas for active (useful) power. In AC circuits, there is also reactive power (generated by capacitors, consumed by coils).

Im– the imaginary part of a complex number (the one with j).

Knowing the reactive and active power, you can calculate the total power of the circuit:

To simplify the calculation of direct and alternating current circuits containing a large number of branches, use one of the simplified methods of circuit analysis. Let's take a closer look at the loop current method.

Loop current method (MCT)

This method is suitable for solving circuits containing more nodes than independent circuits (for example, the circuit from the section on direct current). The principle of the solution is as follows:

This method, like others (for example, the method of nodal potentials, equivalent generator, superposition) is suitable for both direct and alternating current circuits. When calculating alternating current circuits, the resistances of the elements are reduced to a complex form of notation. The system of equations is also solved in complex form.

Literature

Custom Electrical Solution

And remember that our solvers are always ready to help you with TOE. .

Assignment for calculation and graphic work.

For a three-phase circuit in Figure 1, containing non-sinusoidal periodic (T=1/f=1/50=0.02s), emf. e A (t), e B (t), e C (t) of equal amplitude E m, differing from each other only by a time shift by t f =2π/3ω=T/3, it is necessary to obtain:

1. 
   Harmonic composition of phase emfs. – expression of the first three non-zero components from the Fourier series.
2. 
   Instantaneous values ​​of linear voltages.
3. 
   Instantaneous and effective values ​​of phase and linear currents
4. 
   Average load power over the period (total, active, reactive) and power factor.
5. 
   The effective value of the voltage between the zero points of the generator and the load in the event of a break in the neutral wire, having previously converted the circuit into an equivalent star.
6. 
   Using the method of symmetrical components, determine the resistance Z 0 , Z 1 , Z 2 for all components of voltages and currents taken into account during a break in the “ab” phase.

1. Initial data.
Em=180 V; Rab=45 Ohm; Rbc=40 Ohm; Rca=30 Ohm; Cca=75uF; Lab=0.15 Hn;

fundamental harmonic frequency f=50 Hz. Shape of e.m.f. – rectangular.

Load connection diagram:
Figure 1. – Calculated scheme

^ 2. Fourier series expansion.
Obtaining the harmonic composition of phase emfs. We will produce the first three non-zero components from the Fourier series according to the data in our figure:

Figure 2. – Specified non-sinusoidal E.M.F.

Figure 3. – harmonics that make up the voltage eA(t)
Let's find the effective value of the phase voltages:

Figure 4 shows the value
eSt=eAt+eBt+eСt≠0
Its presence confirms the asymmetry of the given system of non-sinusoidal three-phase emf. This value is the sum of all zero-sequence harmonics (in this case, only third-order harmonics).

Instantaneous values ​​of linear voltages:

Let's find the effective value of linear voltages:

^ 3. Calculation of resistances:
To find linear currents, we determine the total complex resistances of the first, third and fifth harmonics.
ab: ,

Let us determine the complex amplitudes of the harmonics of the current phase “ab”:

Let us determine the complex amplitudes of the harmonics of the current phase “bс”:

Let us determine the complex amplitudes of the harmonics of the current phase “ca”:

Instantaneous values ​​of phase currents:

Figure 5. – Phase currents

Effective values ​​of phase currents:

Let us determine the complex amplitudes of the harmonics of the current line “a”:

Let us determine the complex amplitudes of the harmonics of the line “b” current:

Let us determine the complex amplitudes of the harmonics of the line “c” current:

Instantaneous values ​​of line currents:

Figure 6. – linear currents
Effective values ​​of line currents:

^5. Power:
Active power of phase “ab”:

Reactive power of phase “ab”:

Power factor of phase “ab”:

Active power of phase “bc”:

Reactive power of phase “bc”:

Power factor of phase “bc”:

Active power of phase “ca”:

Reactive power of phase “ca”:

Phase power factor “ca”:

Total active power of a three-phase system:

Total reactive power of a three-phase system:

Full power:

Total apparent powers by phase:

Apparent power:

Apparent total power is greater than actual power.

Generalized power factor
^ 6. Neutral displacement calculation:
Converting a triangle to an equivalent star:
Phase “a” resistance:

Phase “b” resistance:

Phase “c” resistance:

Determination of complex voltage amplitudes between neutral points:

Effective neutral offset value:

^ 7. Decomposition into symmetrical components:
Let us choose the “ab” phase break as an emergency situation. Since the potential of points a, b and c depends only on the source parameters, the line voltages will remain unchanged. Consequently, the current in phase “ab” will be equal to zero, and the remaining phase currents will remain unchanged.

Figure 9. – Circuit with a break in phase “a”
Stress decomposition:
First harmonic:

Fifth harmonic:

Current decomposition:
First harmonic:

Fifth harmonic:

Using Ohm's law, we find the total complex resistances of direct, negative and zero sequence:
First harmonic:
Fifth harmonic:

Figure 10. – First voltage harmonic

Figure 11. – Fifth harmonic voltage

Fig12. First harmonic of currents

Fig13. Fifth harmonic currents

Conclusion: In the course of this work, I came to the conclusion that when performing complex calculations such as those presented above, almost absolute accuracy and care are needed, since one small error or inaccuracy entails a series of incorrect results, which has a detrimental effect on ultimately work.

Bibliography

Bessonov L.A. . Textbook - M.: Gardariki 2000, 638 p.

Theoretical foundations of electrical engineering. T.I. Fundamentals of the theory of linear circuits. Ed. P.A. Ionkina. - M.: Higher School, 1976, 544 p.