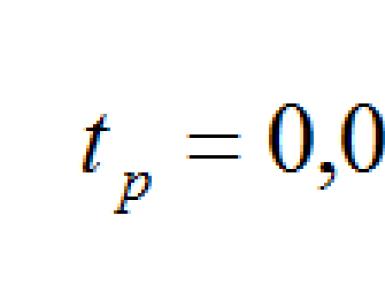Solution 23 of the exam task in computer science

"We solve difficult problems of the Unified State Examination in Informatics"

The purpose of the workshop: consider methodological methods for solving the most complex problems of the exam in computer science.

Presenters: computer science teachers of general educational organizations of the Kostroma region

Attention!!! Seminar participants will receive certificates

Conditions for obtaining a certificate

• Completion of the tasks proposed during the master classes (for all types of tasks)
• Feedback from teachers leading the master class (sending completed tasks to the teacher by e-mail)

Workshop progress

1. Task number 23 of the exam. Solving logical equations in a mirror way

Presenter: Lebedeva Elena Valerievna, teacher of computer science, MBOU of the city of Kostroma "Secondary school No. 21"

• Watch the video materials of the teacher's master class and complete the training tasks. If you cannot view the video materials, then download the presentation and get acquainted with the technology for completing task No. 23.
• [email protected]

Training tasks for part 1 Display method task 1.docx

Training tasks for part 2 Display method task 2.docx

Presentation based on the materials of part 1 and part 2

Training tasks for part 3. display method task 3.docx
Part 3 presentation

2. Task number 5 of the exam. Encoding and decoding data

Presenter: Smirnova Elena Leonidovna, teacher of computer science, secondary school No. 2 of the city district of the city of Bui, Kostroma region

• Watch the video materials of the teacher's master class and complete the training tasks. If you cannot view the video materials, then download the presentation and get acquainted with the technology for completing task No. 5.
• Send the completed training tasks to the teacher by email [email protected]
• Get feedback from your teacher about the results of your work.

Presentation on the demonstrated materials

For effective training in computer science for each task, a brief theoretical material is given to complete the task. More than 10 training tasks with analysis and answers were selected, developed on the basis of the demo version of previous years.

There are no changes in KIM USE 2020 in informatics and ICT.

The areas in which the knowledge test will be carried out:

• Programming;
• Algorithmization;
• ICT tools;
• Information activity;
• Information processes.

Necessary actions when preparing:

• Repetition of the theoretical course;
• Solution tests in informatics online;
• Knowledge of programming languages;
• Pull up mathematics and mathematical logic;
• Use a wider range of literature - the school curriculum for success in the exam is not enough.

Exam Structure

The duration of the exam is 3 hours 55 minutes (255 minutes), of which one and a half hours are recommended to be devoted to completing the tasks of the first part of the KIMs.

Tasks in tickets are divided into blocks:

• Part 1- 23 tasks with a short answer.
• Part 2- 4 tasks with a detailed answer.

Of the proposed 23 tasks of the first part of the examination paper, 12 belong to the basic level of knowledge testing, 10 - to increased complexity, 1 - to a high level of complexity. Three tasks of the second part of a high level of complexity, one - an increased one.

When solving, it is obligatory to record a detailed answer (arbitrary form).
In some tasks, the text of the condition is submitted immediately in five programming languages ​​- for the convenience of students.

Points for tasks in computer science

1 point - for 1-23 tasks
2 points - 25.
3 points - 24, 26.
4 points - 27.
Total: 35 points.

To enter a technical university of an intermediate level, you must score at least 62 points. To enter the metropolitan university, the number of points must correspond to 85-95.

To successfully write an examination paper, you need a clear command of theory and constant practice in solving tasks.

Your formula for success

Work + work on mistakes + carefully read the question from beginning to end to avoid mistakes = maximum score on the exam in computer science.

The lesson considered the decision of task 23 of the exam in computer science: a detailed explanation and analysis of the task of 2017 is given

The 23rd task - "Transformation of logical expressions" - is characterized as a task of a high level of complexity, the execution time is approximately 10 minutes, the maximum score is 1

Elements of the algebra of logic: transformations of logical expressions

To complete task 23 of the exam, it is necessary to repeat the following topics and concepts:

• Consider a topic.
• Consider a topic.

There are 23 different types of tasks and their solution from simple to complex:

1. One equation with non-intersecting operands of the external operation and one solution:

2. One equation with non-intersecting operands of the external operation and several solutions

3. One equation with intersecting operands of the outer operation

Let's consider each case separately and take into account its results for the second equation of the system:

Since for two equations the solutions in three cases cannot “work” simultaneously, the result is the addition of three solutions:

4. Several equations: a method for displaying solutions to an equation

The display method can be used:

5. Multiple Equations: Using Bitmasks

Bitmask (bitmask) is a method that can be used:

Solving 23 USE tasks in computer science

Analysis of the 23 tasks of the Unified State Examination in Informatics 2017 FIPI option 1 (Krylov S.S., Churkina T.E.):

How many different sets of boolean values ​​are there x1, x2, … x6, y1, y2, … y6

(¬(x1 ∨ y1)) ≡ (x2 ∨ y2)
(¬(x2 ∨ y2)) ≡ (x3 ∨ y3)
…
(¬(x5 ∨ y5)) ≡ (x6 ∨ y6)

* A similar task is in the collection "Typical examination options", Krylov S.S., Churkina T.E. 2019 version 7.

¬a ≡ b ¬b ≡ c ¬c ≡ d ¬d ≡ e ¬e ≡ f a ≠ b b ≠ c c ≠ d d ≠ e e ≠ f

Recall what the truth table for equivalence looks like:

x1	x2	F
0	0	1
0	1	0
1	0	0
1	1	1

Let's consider in what cases expressions will return false. Each of the five expressions will be false when: either both operands are true or both operands are false (equivalence = true: at 00 or 11).

Let's make a bitmask for our equations. In the chain of values ​​from a before f there cannot be two ones or two zeros in a row, since in this case the system will be false (for example, a ≠ b, if 0 ≠ 0 - it's a lie). Thus, for these equations, there are only two chains of solutions:

chain 1 chain 2 a 0 1 b 1 0 c 0 1 d 1 0 e 0 1 f 1 0

Now let us recall the substitutions: each of the variables from a before f represents a bracket, inside which two variables are linked disjunction. The disjunction of two variables is true in three cases (01, 10, 11), and false in one (00). That is, for example:

x1 ∨ y1 = 1 when: either 0 ∨ 1 , or 1 ∨ 0 , or 1 ∨ 1 x1 ∨ y1 = 0 if and only if 0 ∨ 0

This means that for each unit in the chain three variant values, and for each zero - one. That. we get:

for the first chain: 3 3 * 1 3 = 27 value sets,

and for the second: 3 3 * 1 3 = 27 value sets

Total sets:

27 * 2 = 54

Result: 54

For a detailed explanation of this task, see the video:

23_2: Analysis of the 23 tasks of the Unified State Examination in Informatics 2017 FIPI option 3 (Krylov S.S., Churkina T.E.):

How many different sets of boolean values ​​are there x1, x2, … x9, y1, y2, … y9 that satisfy all of the following conditions?

(¬(x1 ∧ y1)) ≡ (x2 ∧ y2)
(¬(x2 ∧ y2)) ≡ (x3 ∧ y3)
…
(¬(x8 ∧ y8)) ≡ (x9 ∧ y9)

* A similar task is in the collection "Typical examination options", Krylov S.S., Churkina T.E. 2019 version 9.

✍ Solution (using the bitmask method):

• Since the actions in brackets are the same, and the variables are repeated, we introduce the notation:

¬a ≡ b ¬b ≡ c ¬c ≡ d ¬d ≡ e ¬e ≡ f ¬f ≡ g ¬g ≡ h ¬h ≡ i

Instead of negating the first operand, we'll just use "not equivalent":

a ≠ b b ≠ c c ≠ d d ≠ e e ≠ f f ≠ g g ≠ h h ≠ i

Recall the truth table for equivalence:

x1	x2	F
0	0	1
0	1	0
1	0	0
1	1	1

Now let's consider in which cases the received conditions will return false. Each of the conditions will be false if either both operands are true or both operands are false: For example a ≠ b = 0, if: a=0 and b=0 or a=1 and b=1

This means that for one condition there cannot be such a case that a=0 and b=0 or a=1 and b=1.

Let's compose bitmask for conditions. In the chain of values ​​from a before i there cannot be two ones or two zeros in a row, as in this case the system will be false. Thus, for these conditions, there are only two chains of solutions:

chain 1 chain 2 chain chain a 0 1 0 1 b 1 0 0 1 can not be! c 0 1 ... ... d 1 0 e 0 1 f 1 0 g 0 1 h 1 0 i 0 1

a before i true v one case, and false- v three. That is, for example:

x1 ∧ y1 = 0 when: either 0 ∧ 1 , or 1 ∧ 0 , or 0 ∧ 0 x1 ∧ y1 = 1 if and only if 1 ∧ 1

0 in the chain three 1 - one. That. we get:

for the first chain: 3 5 * 1 4 = 243 value sets,

and for the second: 3 4 * 1 5 = 81 set of values

Total sets:

243 + 81 = 324

Result: 324

We offer to see video with the solution of this 23 task:

23_3: Analysis of the 23 tasks of the Unified State Examination in Informatics 2017 FIPI option 5 (Krylov S.S., Churkina T.E.):

How many different sets of boolean values ​​are there x1, x2, … x8, y1, y2, … y8 that satisfy all of the following conditions?

¬(((x1 ∧ y1) ≡ (x3 ∧ y3)) → (x2 ∧ y2))
¬(((x2 ∧ y2) ≡ (x4 ∧ y4)) → ¬(x3 ∧ y3))
¬(((x3 ∧ y3) ≡ (x5 ∧ y5)) → (x4 ∧ y4))
¬(((x4 ∧ y4) ≡ (x6 ∧ y6)) → ¬(x5 ∧ y5))
¬(((x5 ∧ y5) ≡ (x7 ∧ y7)) → (x6 ∧ y6))
¬(((x6 ∧ y6) ≡ (x8 ∧ y8)) → ¬(x7 ∧ y7))

As an answer, you need to indicate the number of such sets.

* A similar task is in the collection "Typical examination options", Krylov S.S., Churkina T.E., 2019, option 11.

✍ Solution using the bitmask method:

• Since the parentheses are the same actions, and the parentheses are repeated in different equations, we introduce the notation. Let's designate brackets with variables in Latin letters in alphabetical order according to their numbers:

1-a 2-b 3-c 4-d 5-e 6-f 7-g 8-h

After the replacement, we get the following expressions:

¬((a ≡ c) → b) ¬((b ≡ d) → ¬c) ¬((c ≡ e) → d) ¬((d ≡ f) → ¬e) ¬((e ≡ g) → f) ¬((f ≡ h) → ¬g)

Using the laws of the algebra of logic, we transform one of the conditions (the first one). Then, by analogy, we perform transformations for the remaining conditions:

1. Let's get rid of the implication:
It was: ¬((a ≡ c) → b) became: ¬(¬(a ≡ c) ∨ b)
2. According to De Morgan's law, we get rid of the negation over the common outer bracket:
It was: ¬(¬(a ≡ c) ∨ b) became: (a ≡ c) ∧ ¬b

By analogy, we transform the rest of the conditions, given that the double negation simply cancels the negation:

(a ≡ c) ∧ ¬b (b ≡ d) ∧ c (c ≡ e) ∧ ¬d (d ≡ f) ∧ e (e ≡ g) ∧ ¬f (f ≡ h) ∧ g

Let's consider in what cases the conditions will return true. The outer operation is conjunction: each of the conditions will be true only if both operands are true: for example: (a ≡ c) ∧ ¬b will return true if: (a ≡ c) = 1 and ¬b = 1

This means that all operands after the conjunction must be true.

Let's compose bitmask for our equations, taking into account the specified requirement:

chain 1 a ? b 0 c 1 d 0 e 1 f 0 g 1 h ?

Value for variable a find from the condition (a ≡ c) ∧ b. In a bit mask c=1, so that the condition a ≡ c was true a should also equal 1

Value for variable h find from the condition (f ≡ h) ∧ ¬g. In a bit mask f=0, so that the condition f ≡ h was true h should also equal 0 (equivalence truth table).

Get the final bitmask:

chain 1 a 1 b 0 c 1 d 0 e 1 f 0 g 1 h 0

Now remember that each of the variables from a before h is a bracket containing two variables connected by a conjunction. Conjunction of two variables true v one case, and false- v three. That is, for example:

x1 ∧ y1 = 0 when: either 0 ∧ 1 , or 1 ∧ 0 , or 0 ∧ 0 x1 ∧ y1 = 1 if and only if 1 ∧ 1

This means that for each 0 in the chain three variant values, and for each 1 - one. Thus, we get:

3 4 * 1 4 = 81 set of values

Result: 81

23_4: Analysis of the 23 tasks of the USE in informatics demo version of 2018 FIPI:

How many different sets of boolean values ​​are there x1, x2, … x7, y1, y2, … y7 that satisfy all of the following conditions?

(¬x1 ∨ y1) → (¬x2 ∧ y2) = 1
(¬x2 ∨ y2) → (¬x3 ∧ y3) = 1
…
(¬x6 ∨ y6) → (¬x7 ∧ y7) = 1

✍ Solution, display method used:

• An external operation in a single equation is an implication, the result of which must be true. The implication is true if:

0 -> 0 0 -> 1 1 -> 1

those. false only when 1 -> 0

If the bracket (¬x1 ∨ y1) = 0 , then for the bracket (¬x2 ∧ y2) there are options 0 or 1 .

If the bracket (¬x1 ∨ y1) = 1 , then for the bracket (¬x2 ∧ y2) one option is possible - 1 .

In brackets, the disjunction (∨) is true when: 0 ∨ 1, 1 ∨ 0, 1 ∨ 1; false when: 0 ∨ 0.

In brackets, the conjunction is true when 1 ∧ 1 and false in all other cases.

Let's build a truth table for the first equation, consider all possible options. Let's select in it those lines that return false: i.e. where is the first parenthesis (¬x1 ∨ y1) will return 1 , and the second (¬x2 ∧ y2)— 0 :

Since the equations are of the same type and differ only in the shift of the numbers of variables by one, we will use the mapping method. For the first equation x1 and y1 will be designated x i and y i, a x2 and y2 will be designated x i+1 and yi+1.

Now we find the total number of solutions by substituting the corresponding x and y

As a result, we get:

1 + 19 + 1 + 1 = 22

Result: 22

Video analysis of the demo version 2018 23 tasks, see here:

23_5: Solution 23 of the USE task in informatics 2018 (diagnostic option, S.S. Krylov, D.M. Ushakov, USE simulator 2018):

How many different solutions does the equation have:

(a → b) ∨ (c → ¬d) ∨ ¬(e ∨ a ∨ c) = 1

where a, b, c, d, e- Boolean variables?

As an answer, indicate the number of such sets.

✍ Solution:

• External logical operation − ∨ - disjunction. Truth table:

0 ∨ 0 = 0 0 ∨ 1 = 1 1 ∨ 0 = 1 1 ∨ 1 = 1

Since the disjunction is equal to one even in three cases, it will be quite difficult to search for the number of options. Much easier to find options when ∨ = 0 and subtract them from the total number of options.

Find the total number of rows in the truth table. There are 5 variables in total, so:

number of rows in TableTrue = 2 5 = 32

Let's calculate how many options have a solution when the value of the equation = 0. To then subtract this value from the total. For the disjunction (∨) operation, each parenthesis must be equal to zero:

(a → b) ∨ (c → ¬d) ∨ ¬(e ∨ a ∨ c) = 0 0 0 0

Now consider each bracket separately:

1. (a → b) = 0, the implication is false in one case (1 → 0) = 0 i.e. we have a = 1, b = 0 2. (c → ¬d) = 0, the implication is false in one case (1 → 0) = 0 i.e. we have c = 1, d=1 3. ¬(e ∨ a ∨ c) = 0

because there is a negation in front of the bracket, then for greater clarity, we will open the brackets according to De Morgan's law:

¬e ∧ ¬a ∧ ¬c = 0 The conjunction is 0 when at least one operand = 0.

from item 1 and item 2 we have a = 1 and c = 1. Then for e we have two options: e = 0, e = 1, i.e.:

¬0 ∧ ¬1 ∧ ¬1 = 0 ¬1 ∧ ¬1 ∧ ¬1 = 0

That is, in total we have 2 chains of “excluded” solutions:

1. a = 1, b = 0, c = 1, d = 1, e = 0 2. a = 1, b = 0, c = 1, d = 1, e = 1

These two options are excluded (subtracted) from the total:

32 - 2 = 30

Result: 30

23_6: Analysis of 23 tasks of the demo version of the exam in informatics 2019:

How many different sets of boolean values ​​are there x1, x2, … x7, y1, y2, … y7 that satisfy all of the following conditions?

(y1 → (y2 ∧ x1)) ∧ (x1 → x2) = 1 (y2 → (y3 ∧ x2)) ∧ (x2 → x3) = 1 … (y6 → (y7 ∧ x6)) ∧ (x6 → x7) = 1 y7 → x7 = 1

In response no need list all different sets of values ​​of the variables x1, x2, … x7, y1, y2, … y7, under which the given system of equalities is satisfied.
As an answer, you need to indicate the number of such sets.

✍ Solution:

• Since all equalities are of the same type (except the last one), they differ only in the shift of the numbers of variables by one, then for the solution we will use the mapping method: when, having found the result for the first equality, it is necessary to apply the same principle with subsequent equalities, taking into account the results obtained for each of them.
• Consider the first equality. In it, the outer operation is a conjunction, the result of which must be true. The conjunction is true if:

1 -> 1 i.e.: (y1 → (y2 ∧ x1)) ∧ (x1 → x2) = 1 1 1

Find cases where the equality is false (in order to exclude these cases in the future):

(y1 → (y2 ∧ x1)) ∧ (x1 → x2) = 0

Inside the first "big" parenthesis is the operation of implication. Which is false:

1 -> 0 = 0 i.e. cases: y1=1 → (y2=0 ∧ x1=1) y1=1 → (y2=1 ∧ x1=0) y1=1 → (y2=0 ∧ x1=0)

Let's analyze the second bracket in the same way. In it, the implication will return false:

(x1=1 → x2=0)

Let's build a truth table for the first equation, consider all possible options. Since there are 4 variables, there will be 2 4 = rows 16 . Select those lines that return false:

Now let's move on to the display method. For the first equation x1 and y1 denote x i and y i, a x2 and y2 denote x i+1 and yi+1. Arrows denote the values ​​of only those rows of the truth table that return 1 .

Let's find the total number of solutions by substituting the corresponding values ​​into the table from the display x and y, and given the previous values:

Now back to the last equality. By definition, it must be true. Equality will return false in only one case:

y7=1 → x7=0 = 0

Let's find the corresponding variables in our table:

Calculate the sum over the last column, ignoring the line that returns false:

1 + 7 + 28 = 36

Result: 36

Video solution for 23 tasks of the demo version of the exam 2019:

23_7: Analysis of 23 tasks of the Unified State Examination in Informatics “Typical examination options”, Krylov S.S., Churkina T.E., 2019, option 16 (FIPI):

How many different sets of boolean values ​​are there x1, x2, … x6, y1, y2, … y6 that satisfy all of the following conditions?

¬(((x1 ∧ y1)) ≡ (x2 ∧ y2)) → (x3 ∧ y3))
¬(((x2 ∧ y2)) ∨ ¬(x3 ∧ y3)) → (x4 ∧ y4))
¬(((x3 ∧ y3)) ≡ (x4 ∧ y4)) → (x5 ∧ y5))
¬(((x4 ∧ y4)) ∨ ¬(x5 ∧ y5)) → (x6 ∧ y6))

As an answer, you need to indicate the number of such sets.

✍ Solution:

• Since in small brackets the same operation is everywhere ( ∧ ), and the variables in the brackets do not intersect, then you can perform the replacement:

¬((a ≡ b) → c) = 1 ¬((b ∨ ¬c) → d) = 1 ...

Let's get rid of the negation by pointing out that each expression becomes false:

(a ≡ b) → c = 0 (b ∨ ¬c) → d = 0 (c ≡ d) → e = 0 (d ∨ ¬e) → f = 0

The outer operation in all expressions is the implication ( → ). Recall the truth table for the implication operation:

0 → 0 = 1 0 → 1 = 1 1 → 0 = 0 1 → 1 = 1

The implication is false only in one case: 1 → 0 = 0 . All expressions in the task are false. Let's learn this.

Let's build a bitmask by tracing the value of each variable, moving from the first expression to the last:

chain1 chain2 a 0 1 b 0 1 c 0 0 d 0 0 e 0 0 f 0 0

Since each variable initially replaces the bracket in which the conjunction operation (∧) is located, then, remembering the truth table for this operation, we compare 3 solutions for each zero (the conjunction is false in three cases), and for each unit - 1 solution (the conjunction is true in one case).

Let's calculate the value for each bitstring:

chain1 = 3*3*3*3*3*3 = 729 solutions chain2 = 1*1*3*3*3*3 = 81 solutions

Since the chains cannot be executed simultaneously, but either one or the other will be executed, the resulting values ​​\u200b\u200bmust be added:

729 + 81 = 810 solutions

Answer: 810

Video analysis of task 23 is available:

23_8: Analysis of 23 tasks of the Unified State Examination in Informatics “Typical examination options”, Krylov S.S., Churkina T.E., 2019, option 2 (FIPI):

How many different sets of boolean values ​​are there x1, x2, … x12 that satisfy all of the following conditions?

¬(x1 ≡ x2) → (x3 ∧ x4) = 0
¬(x3 ≡ x4) → (x5 ∧ x6) = 0
¬(x5 ≡ x6) → (x7 ∧ x8) = 0
¬(x7 ≡ x8) → (x9 ∧ x10) = 0
¬(x9 ≡ x10) → (x11 ∧ x12) = 0
(x1 ≡ x4) ∨ (x5 ≡ x8) ∨ (x2 ≡ x12) = 1

As an answer, you need to indicate the number of such sets.

✍ Solution:

x1 x2 x4 x5 x8 x12 0 0 1 0 1 1 0 1 1 0 1 0 0 0 1 1 0 1 0 1 1 1 0 0 1 0 0 0 1 1 1 1 0 0 1 0 1 0 0 1 0 1 1 1 0 1 0 0

Since in the mapping scheme the values ​​for the pair x1 and x2 equal 00 and 11 are not used, then we select them and will not use them in subsequent calculations. Let's write down the remaining options:

x1 x2 x4 x5 x8 x12 0 1 1 0 1 0 y1 0 1 1 1 0 0 y2 1 0 0 0 1 1 y3 1 0 0 1 0 1 y4

Let's build a mapping table separately for each resulting row, taking into account the values ​​of the operands (x n):

Let's count the number of solutions for all received rows: 4 + 4 + 2 + 2 = 12

These solutions must be excluded, because we considered a false case equations 6:

96 - 12 = 84

Job directory.
Systems of logical equations containing equations of the same type

Sorting Basic Easy first Hard first Popularity Newest first Oldest first
Take the test for these tasks
Back to job catalog
Version for printing and copying in MS Word

How many there are different sets of values ​​of log-gi-che-changes x1, x2, x3, x4, x5, x6 , x7, x8 someone satisfies all the above-numbers below the conditions?

(x1≡x2)->(x2≡x3) = 1

(x2≡x3)->(x3≡x4) = 1

(x6≡x7)->(x7≡x8) = 1

In from-ve-those no need re-re-number all the different sets of values ​​\u200b\u200bof changes x1, x2, x3, x4, x5, x6, x7, x8 with someone ryh you-half-not-on this system of equalities. In the quality of from-ve-ta, you need to indicate the number of such sets of ditches.

Solution.

Let's write the variables in a line: x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 . An implication is false only if the truth implies a lie. The condition is not met if there is another digit in the row after a pair of identical digits. For example, "11101...", which means that the second condition is not met.

Consider combinations of variables that satisfy all conditions. Let's write out the options in which all the digits alternate, there are two of them: 10101010 and 01010101. Now for the first option, starting from the end, we will increase the number of consecutive digits (as much as possible). Let's write down the resulting combinations: “1010 1011; 1010 1111; 1011 1111; 1111 1111; 1010 1000; 1010 0000; 1000 0000; 0000 0000” there are nine such combinations, including the original one. Similarly for the second option: “0101 0101; 0101 0100; 0101 0000; 0100 0000; 0000 0000; 0101 0111; 0101 1111; 0111 1111; 1111 1111 "- there are also nine such combinations. Note that the combinations 0000 0000 and 1111 1111 are counted twice. Thus, we get 9 + 9 − 2 = 16 solutions.

Answer: 16.

Answer: 16

¬(x 1 ≡ x 2) ∧ (x 1 ∨ x 3) ∧ (¬x 1 ∨ ¬x 3) = 0

¬(x 2 ≡ x 3) ∧ (x 2 ∨ x 4) ∧ (¬x 2 ∨ ¬x 4) = 0

¬(x 8 ≡ x 9) ∧ (x 8 ∨ x 10) ∧ (¬x 8 ∨ ¬x 10) = 0

In response no need

Solution.

Consider the first equation.

For x 1 \u003d 1, two cases are possible: x 2 \u003d 0 and x 2 \u003d 1. In the first case, x 3 \u003d 1. In the second, x 3 is either 0 or 1. For x 1 \u003d 0, two cases are also possible: x 2 \u003d 0 and x 2 \u003d 1. In the first case, x 3 is either 0 or 1. In the second, x 3 \u003d 0. Thus, the equation has 6 solutions (see figure).

Consider a system of two equations.

Let x 1 = 1. For x 2 = 0, only one case is possible: x 3 = 1, variable x 4 = 0. For x 2 = 1, two cases are possible: x 3 = 0 and x 3 = 1. In the first case, x 4 = 1, in the second - x 4 or 0 or 1. We have 4 options in total.

Let x 1 = 0. For x 2 = 1, only one case is possible: x 3 = 0, variable x 4 = 1. For x 2 = 0, two cases are possible: x 3 = 0 and x 3 = 1. In the first case, x 4 is either 1 or 0, in the second - x 4 \u003d 0. We have 4 options in total.

Thus, the system of two equations has 4 + 4 = 8 options (see figure).

A system of three equations will have 10 solutions, of four - 12. A system of eight equations will have 20 solutions.

Answer: 20

Source: USE in Informatics 05/30/2013. main wave. Centre. Option 1.

How many different sets of values ​​for boolean variables x 1 , x 2 , ... x 10 are there that satisfy all of the following conditions?

(x 1 ∧ ¬x 2) ∨ (¬x 1 ∧ x 2) ∨ (x 3 ∧ x 4) ∨ (¬x 3 ∧ ¬x 4) = 1

(x 3 ∧ ¬x 4) ∨ (¬x 3 ∧ x 4) ∨ (x 5 ∧ x 6) ∨ (¬x 5 ∧ ¬x 6) = 1

(x 7 ∧ ¬x 8) ∨ (¬x 7 ∧ x 8) ∨ (x 9 ∧ x 10) ∨ (¬x 9 ∧ ¬x 10) = 1

In response no need list all different sets of values ​​of variables x 1 , x 2 , … x 10 for which the given system of equalities is satisfied. As an answer, you need to indicate the number of such sets.

Solution.

The first equation has 12 solutions. The second equation is related to the first only through the variables x 3 and x 4 . Based on the decision tree for the first equation, we write out the pairs of values ​​of the variables x 3 and x 4 that satisfy the first equation and indicate the number of such pairs of values.

Quantity value pairs	x 3	x4
×4	1	1
×4	0	0
×2	1	0
×2	0	1

Since the equations are identical up to the indices of the variables, the decision tree of the second equation is similar to the first. Therefore, the pair of values ​​x 3 = 1 and x 4 = 1 generates two sets of variables x 3 , ..., x 6 satisfying the second equation. Since there are four pairs of these solutions among the sets of solutions of the first equation, we get 4 · 2 = 8 sets of variables x 1 , ..., x 6 satisfying the system of two equations. Arguing similarly for a pair of values ​​x 3 = 0 and x 4 = 0, we obtain 8 sets of variables x 1 , ..., x 6 . The pair x 3 = 1 and x 4 = 0 generates four solutions to the second equation. Since there are two of these pairs among the sets of solutions of the first equation, we obtain 2 · 4 = 8 sets of variables x 1 , ..., x 6 satisfying the system of two equations. Similarly for x 3 = 0 and x 4 = 1 - 8 sets of solutions. In total, the system of two equations has 8 + 8 + 8 + 8 = 32 solutions.

Having carried out similar reasoning for a system of three equations, we obtain 80 sets of variables x 1 , ..., x 8 that satisfy the system. for a system of four equations, there are 192 sets of variables x 1 , ..., x 10 that satisfy the system.

Answer: 192.

Answer: 192

Source: Unified State Examination in Informatics 07/08/2013. Second wave. Option 501.

a guest 17.12.2013 18:50

We counted 3 times, it turns out that after 2 equations there are 34 solutions, and you have 32, we have 8 + 12 + 8 + 6, and you have 8 + 8 + 8 + 8

Petr Murzin

Give your solution in full. Write how you get 12 and 6.

Ivan Grebenshchikov 12.06.2016 20:51

In general, this problem can be solved much easier. If we notice (x1 ∧ ¬x2) ∨ (¬x1 ∧ x2) identically ¬(x1 == x2) and (x3 ∧ x4) ∨ (¬x3 ∧ ¬x4) identically (x3 == x4), then, substituting into the original equation, we get: ¬(x1 == x2) ∨ (x3 == x4) = 1. However, this expression can also be transformed and get (x1 == x2) → (x3 == x4) = 1.

Transforming all expressions in a similar way, we get:

(x1 == x2) → (x3 == x4) = 1

(x3 == x4) → (x5 == x6) = 1

(x7 == x8) → (x9 == x10) = 1

Replacing (x1 == x2) with A1, (x3 == x4) with A3, ... , (x9 == x10) with A9, we obtain sets of solutions for A-items:

A1 A3 A5 A7 A9

Each A-total corresponds (regardless of value) to a pair of pairs of values ​​of the i-th and i + 1 -th x-th => (2 * 2 * 2 * 2 * 2) * 6 (since there are six sets of solutions for A- total) = 192

How many different sets of values ​​for boolean variables x 1 , x 2 , ... x 10 are there that satisfy all of the following conditions?

(x 1 ∧ x 2) ∨ (¬x 1 ∧ ¬x 2) ∨ (¬x 3 ∧ x 4) ∨ (x 3 ∧ ¬x 4) = 1

(x 3 ∧ x 4) ∨ (¬x 3 ∧ ¬x 4) ∨ (¬x 5 ∧ x 6) ∨ (x 5 ∧ ¬x 6) = 1

(x 7 ∧ x 8) ∨ (¬x 7 ∧ ¬x 8) ∨ (¬x 9 ∧ x 10) ∨ (x 9 ∧ ¬x 10) = 1

In response no need list all different sets of values ​​of variables x 1 , x 2 , … x 10 for which the given system of equalities is satisfied. As an answer, you need to indicate the number of such sets.

Solution.

Let's build a decision tree for the first equation.

Thus, the first equation has 12 solutions.

The second equation is related to the first only through the variables x 3 and x 4 . Based on the decision tree for the first equation, we write out the pairs of values ​​of the variables x 3 and x 4 that satisfy the first equation and indicate the number of such pairs of values.

Quantity value pairs	x 3	x4
×2	1	1
×2	0	0
×4	1	0
×4	0	1

Since the equations are identical up to the indices of the variables, the decision tree of the second equation is similar to the first (see the figure). Therefore, the pair of values ​​x 3 = 1 and x 4 = 1 generates four sets of variables x 3 , ..., x 6 satisfying the second equation. Since there are two pairs of these pairs among the sets of solutions of the first equation, in total we get 4 · 2 = 8 sets of variables x 1 , ..., x 6 satisfying the system of two equations. Arguing similarly for a pair of values ​​x 3 = 0 and x 4 = 0, we obtain 8 sets of variables x 1 , ..., x 6 . The pair x 3 = 1 and x 4 = 0 generates two solutions to the second equation. Since there are four of these pairs among the sets of solutions of the first equation, we obtain 2 · 4 = 8 sets of variables x 1 , ..., x 6 satisfying the system of two equations. Similarly for x 3 = 0 and x 4 = 1 - 8 sets of solutions. In total, the system of two equations has 8 + 8 + 8 + 8 = 32 solutions.

The third equation is related to the second only through the variables x 5 and x 6 . The decision tree is similar. Then for a system of three equations, each pair of values ​​x 5 and x 6 will generate a number of solutions according to the tree (see figure): pair (1, 0) will generate 2 solutions, pair (1, 1) will generate 4 solutions, and etc.

From the solution of the first equation, we know that the pair of values ​​x 3 , x 4 (1, 1) occurs twice in the solutions. Therefore, for a system of three equations, the number of solutions for the pair x 3 , x 4 (1, 1) is 2 · (2 ​​+ 4 + 4 + 2) = 24 (see Fig.). Using the table above, we calculate the number of solutions for the remaining pairs x 3 , x 4:

4 (2 + 2) = 16

2 (2 + 4 + 4 + 2) = 24

4 (2 + 2) = 16

Thus, for a system of three equations, we have 24 + 16 + 24 + 16 = 80 sets of variables x 1 , ..., x 8 that satisfy the system.

For a system of four equations, there are 192 sets of variables x 1 , ..., x 10 that satisfy the system.

Answer: 192.

Interactive simulator 23 USE DEMO 2017

for those who are at a loss, the full solution is located at the very end of this page

If you have any questions, doubts or remarks, write ...

And the second one with the condition expanded by me specifically for underlining apparent complexity and huge difference , how number of equations , and their content .

Demonstration version of the USE 2015 informatics and ICT task 23.

How many different sets of values ​​of boolean variables x1, x2, ... x8, y1, y2, ... y8 are there that satisfy all of the following conditions?
(x1 | x2) & ((x1 & x2) → x3) & (¬x1 | y1) = 1
(x2 | x3) & ((x2 & x3) → x4) & (¬x2 | y2) = 1
(x3 | x4) & ((x3 & x4) → x5) & (¬x3 | y3) = 1
(x4 | x5) & ((x4 & x5) → x6) & (¬x4 | y4) = 1
(x5 | x6) & ((x5 & x6) → x7) & (¬x5 | y5) = 1
(x6 | x7) & ((x6 & x7) → x8) & (¬x6 | y6) = 1
(x7 | x8) & (¬x7 | y7) = 1
(¬x8 | y8) = 1

In your answer, you do not need to list all the different sets of values ​​of the variables x1, x2, ... x8, y1, y2, ... y8, under which this system of equations is satisfied. As an answer, you need to indicate the number of such sets.

And it only remains for me, despite this very apparent complexity of this task, to show. how its solution can easily be reduced to a solution similar to the first.

We take the first equation (x1 | x2) & ((x1 & x2) → x3) & (¬x1 | y1) = 1 and use the truth table to find all its solutions. After that, it remains to select (delete) all rows that have 0 in the final column

Analyzing the table, we build mappings of pairs x 1x 2 to x 2x 3, noticing that the first pair with values ​​01 is mapped to the second with value 10 twice (for valuey 1=1 andy 1=0 hence the double red arrow, the mapping is similarly constructed for pairs with values ​​01-11)

According to this figure, we build mapping rules, according to which we find the number of solutions for the first six equations, for which it is enough to fill in the following table

From where we find that the first six equations have only 53 solutions.

And it remains for us to deal with the remaining "additional" two equations
(x7 | x8) & (¬x7 | y7) = 1
(¬x8 | y8) = 1
Let us dwell on the first of them and, without going into deep reasoning, fill in the truth table for it, where the number 1 denotes conditionally the first bracket, and the number two, respectively, the second and the lid, their product.

The table shows that the pair x7x8

has no solutions for values ​​00 (which means the following: x7x8 pair with value 00 will be displayed in y7 with the same values ​​0 times (i.e. not displayed)

has two solutions at value 01 (y7 = 0 and y7 = 1 , which means the following: the number of solutions for the pair x7x8 with value 01, appearing in y7 - will double

has one solution each with values ​​10 and 11 , i.e. the number of solutions in the mapping with these values ​​will not change.

It remains for us, by filling in the corresponding cells with the found values, to find the number of solutions for the first seven equations

And here it is, the most crucial step, therefore, in order not to make unnecessary mistakes, we again resort to constructing a truth table, but for the eighth equation
(¬x8 | y8) = 1

From our truth table, we can see that

if X8 = 0, then Y8 has two solutions 0 and 1 (i.e., the number of solutions is doubled when displaying)

if X8 = 1, then Y8 has one solution (i.e. the number of solutions when displayed is unchanged)

this means that if x8 is 0, then in the mapping x8 to y8 for values ​​00 and 10 the number of solutions is doubled, and in the case when x8 is 1 in the mapping x8 to y8 for values ​​01 and 11 the number of solutions remains unchanged. This is what we will display in the final table and summing up all the values ​​of the column Y8 find the desired result.

Correct answer: 61

A complete solution-hint for task 23 of the Unified State Examination Demo 2017 in Informatics